• Expert Maths Tuition That Builds Confidence, Clarity, and Top Results

  Personalised maths tuition for students aged 11+ — from GCSE and A-Level to university level — across all exam boards.

  Choose between weekly lessons or intensive courses, tailored to your goals, timetable, and learning style.

  ✔ Proven, high-success teaching methods developed over 25 years
  ✔ Specialist in making difficult topics simple and intuitive
  ✔ Trusted by parents and students with outstanding results
  ✔ Online or face-to-face tuition available
  ✔ Maths & STEM school teacher and Associate Lecturer in Maths & Engineering
  ✔ DBS checked

   Book a free consultation or enquire today to discuss the best option for your child.

I teach maths in a clear, intuitive way that focuses on understanding rather than memorisation. By breaking complex ideas into simple patterns and logical steps, students quickly gain confidence, fluency, and the ability to solve unfamiliar problems independently.

Most students notice a clear improvement within the first few lessons.

A Different Way of Learning Maths

Many private tutors simply repeat the same methods used in schools. If those approaches were already working, additional tuition would rarely be necessary.

I teach maths in a fundamentally different way.

My approach is built on intuition rather than memorisation, understanding rather than rote procedures, and problem-solving rather than mechanical repetition. The aim is to help students see how maths works, so they can tackle unfamiliar questions with confidence.

This method grew from my own frustration with how mathematics is commonly taught and has been refined over 25 years of working with students of all abilities.

What Makes My Method Different

✔ Clear, efficient techniques that dramatically simplify arithmetic and algebra
✔ A small set of underlying principles that connect large areas of mathematics
✔ Visual and numerical explanations before introducing formal algebra
✔ Faster, more reliable mental and written calculation strategies
✔ Alternative ways of solving equations that reveal meaning, not just answers
✔ Deeper conceptual understanding of topics such as indices, quadratics, trigonometry, and graphs

These methods allow students to progress more quickly while developing genuine understanding rather than surface-level exam tricks.

For A-Level and Advanced Students

In addition to the above, students develop:

✔ A deep, intuitive understanding of differentiation and integration
✔ Clear insight into where key formulas come from and why they work
✔ Powerful approaches to binomial expansion, quadratics, and higher powers
✔ Broader and more flexible uses of core ideas such as Pythagoras’ theorem
✔ Strong foundations for further study in mathematics, engineering, and STEM subjects

Who This Helps Most

I regularly work with students who:

• Have lost confidence

• Feel maths “doesn’t make sense”

• Understand in lessons but struggle in exams

• Feel anxious or overwhelmed

• Dislike or avoid maths

Using my method, these students typically experience rapid improvements in clarity, confidence, and results.

I also work successfully with high-ability students, helping them deepen their understanding, make powerful connections between topics, and accelerate through material.

Results

This approach has produced consistently high success rates, including years where every examined student achieved their target outcome. Most students come to me because standard teaching has not worked for them — and leave with a completely different relationship with maths.

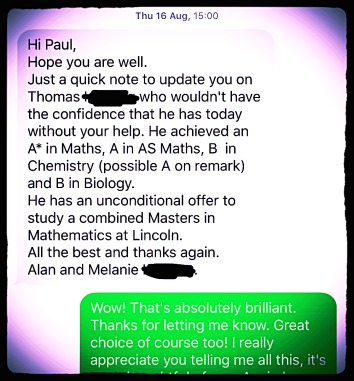
ABOVE: I was extremely gratified and pleased to receive this message after the GCSE results of 2016. 

(See below for update in 2018!)

Even More About My Method

Over 25 years, I have developed a unique method for teaching mathematics that is built around the psychology of learning. It continues to evolve to become more efficient, more intuitive, and more connected.

Rather than using many disconnected techniques, my approach focuses on a small number of powerful ideas used frequently, which reduces cognitive load and builds fluency. I place strong emphasis on explaining the why behind every concept, so students understand what they are doing instead of memorising steps.

This deeper understanding transforms how students experience maths.

Recognition and Global Reach

My method has been published by the UK’s largest educational publisher and is available in print and Kindle editions. I regularly receive messages from students and adults around the world who describe finally experiencing a breakthrough after years of struggle.

I have also created an online video library so students can revisit explanations as often as they need, reinforcing learning between lessons.

What I See Every Day

The most rewarding part of my work is watching students realise they can understand maths — often for the first time.

In a calm, supportive, and positive environment, students regularly achieve results that surprise both themselves and their parents. Many go on to perform well beyond their expected level.

My method improves mathematical ability at any starting point while also helping students rebuild confidence, self-belief, and self-respect.

A Teacher Who Still Learns

I am deeply passionate about learning and deliberately continue to study so I never lose sight of what it feels like to be a student.

Alongside teaching, I have completed a second engineering degree with the Open University, undertaken technical and professional training, and continue to study advanced mathematics and languages. This ongoing learning directly informs and strengthens my teaching.

Intensive Courses and Programmes

In addition to weekly tuition, I offer:

• 5 or 7-day intensive GCSE courses

• 14-day intensive A-Level courses

These focused programmes are highly effective and fully resourced. Delivery can be online or in person.

I am confident enough in the approach to guarantee the requested grade for intensive courses.

Next Step

The best way to explore whether my approach is right for your child is a conversation.

Please get in touch via the contact form or phone, and I will respond as promptly as possible.

Paul Carson BSc BEng (Hons) AMIMA

Selection of Qualifications

Bachelor of Engineering - BEng (Hons) (Open) 2020

BSc Pure Science (University of St Andrews) - 2002

A at A-Level Maths 

A* at GCSE Maths

Level 3 Award in Teaching and Education - 2016

NVQ in Aeronautical Engineering

Current Projects:

Running virtually from Lincoln to Auschwitz Concentration Camp as a tribute to victims and survivors. 

Learning the Polish and Irish (Gaeilge) languages.

Tutoring Experience: 

25 years as a private tutor of all ages from 10 upwards with some school experience in Lincolnshire. I estimate I have taught over 10,000 hours in that time. 

3 years as an Associate Lecturer with the Open University in Maths and Engineering. I am responsible for around 40 adult students per year. 

Our Initial Meeting... 

My approach is to first identify any issues the student has via an assessment. From this I can develop a strategy for the student to understand maths more easily, which they can take on board to increase in confidence, knowledge and ability. The student will begin to find maths much more easy than they had previously thought. The normal pattern is that the student has failed by using school techniques, so repeating more of the same won't work! My methods are logical, easy and intuitive.